멱급수의 수렴성 (convergence of power series)
2022. 11. 8. 18:44ㆍ뚝딱이의 공부/미분과 적분
아래와 같은 멱급수가 주어졌을 때, 아래의 멱급수가 수렴할 지를 판단해보자
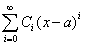
상황 1. (n+1번째 항)을 (n번째 항)으로 나눈 값의 극한 값이 -1과 1 사이에 있는 경우 -> 절대수렴
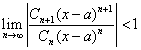
이럴 경우 주어진 멱급수는 '절대수렴' 한다.
상황 1을 달리 표현하면,
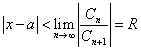
즉, 아래와 같은 조건일 때, 주어진 멱급수는 절대수렴한다.
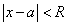
a나 Cn이 정해져 있다면, 위 멱급수가 수렴하는 x 값의 범위를 알 수 있다.
R은 '수렴반경' 이라고 한다.
상황 2. (n+1번째 항)을 (n번째 항)으로 나눈 값의 극한 값의 절댓값이 1보다 큰 경우 -> 발산
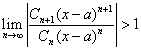
이 경우, 주어진 멱급수는 '발산' 한다.
즉, 아래와 같은 조건일 때, 주어진 멱급수는 발산한다.
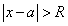
상황 3. (n+1번째 항)을 (n번째 항)으로 나눈 값의 극한 값의 절댓값이 1인 경우 -> 결정 못함(no decision)
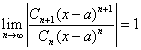
이 경우, 주어진 멱급수의 수렴여부를 판단하는 것은 어렵다. (다른 방법을 사용하여 풀 수도 있음, 못 풀 수도 있고..)
이 경우 조건은 다음과 같다.
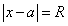
'뚝딱이의 공부 > 미분과 적분' 카테고리의 다른 글
| 곡률 공식 증명 (0) | 2023.01.03 |
|---|---|
| 파이 값을 구하는 법 (Maclaurin 함수 이용) (0) | 2022.11.13 |
| 멱급수(power series)의 정의 (0) | 2022.11.08 |
| 1/(1-x)에 대한 멱급수 표현 (0) | 2022.11.04 |
| 로피탈 정리 (0) | 2022.11.04 |